In this page, we will fully specify the actual workings of Melmint on the Themelio blockchain. This is in contrast to the whitepaper, which only provides a high-level design.

We call the mechanism Melmint v2 because it has some several important differences with the “paper” Melmint version.

Introduction

“Paper Melmint”

In our original publication, Melmint is divided into two halves:

• A DOSC/sym auction that establishes a DOSC/sym exchange rate
• A mel/sym exchange guarantee that allows anybody to destroy 1 mel in exchange for $k$ DOSC worth of newly printed syms, or vice versa, minus a small fee.

The following picture illustrates “paper Melmint”:

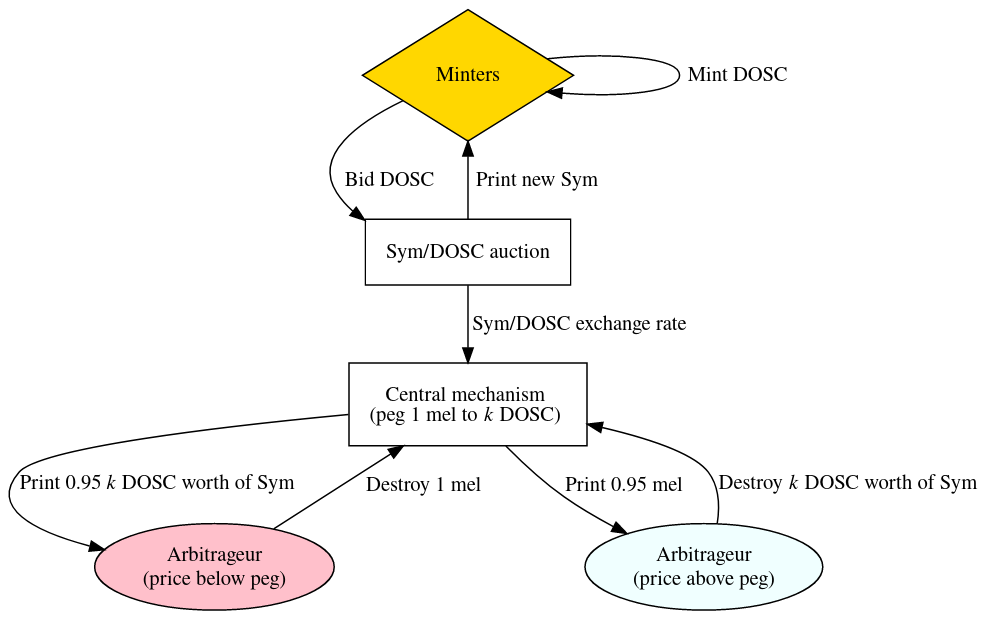
The central idea is that through auctioning off a steady stream of sym for DOSC, we know how much computation a sym is worth. We can then “back” mels with $k$ DOSC worth of newly printed sym.

This way, the “collateral” of a mel is simply the value that can be extracted through diluting syms. Comparisons with existing economies seem to indicate that runs on mels are unlikely because the sym will have significantly higher market cap, but nevertheless “paper Melmint” has a fairly complex system that detects runs and devalues the mel by adjusting $k$ downwards.

Problems with “paper Melmint”

Unfortunately, paper Melmint has some significant downsides that make it impractical to implement on Themelio:

• It requires many different transaction types: at least DoscMint (minting DOSC), AuctionBid (for bidding in the auction), AuctionBuyout (for “buying out” others' bids from the order book), AuctionFill (generated automatically to award the sym to the highest bidder), and Swap (to swap between sym and mel). This is clunky and inelegant, and our abortive attempt at implementing “paper Melmint” caused a huge fraction of our transaction processing code to be solely devoted to Melmint.
• Auctions are notoriously tricky to get right. Although the addition of “auction buyouts” (which also complicates implementation) probably makes it hard to game the “oracle” derived from the DOSC/sym auction, participants will still need to do a lot of tricky strategizing. Furthermore, the 20-block auction period makes frontrunning, “blockchain clock” inaccuracy, etc very problematic.
• Demurrage is tricky. DOSCs are supposed to have demurrage, or a face value that decays over time. This is tricky to implement in Themelio’s strict UTXO model, without lots of special casing for DOSCs.

Thus, Melmint v2, while keeping the core idea of paper Melmint, completely revamps the specifics of how the mel/DOSC peg is maintained. The auction with a general swapping mechanism, and demurrage is replaced with DOSC inflation.

An overview of Melmint v2

Melmint v2 is based on Melswap, a Uniswap v1-inspired “token swapping” mechanism built into Themelio. All non-mel tokens can be swapped with Mel using Melswap, and a liquidity provider reward mechanism incentivizes participation.

There is no more sym auction or inbuilt sym inflation. Instead, we simply use the DOSC/mel and DOSC/sym pairs in Melswap to derive the appropriate mel/sym exchange rate. Every block, more Mel or more Sym will printed and stuffed into the mel/sym pool in order to target the correct mel/sym exchange rate.

Why not directly target the DOSC/mel pair? Because we can’t let the protocol print DOSCs, lest they no longer become DOSCs. Using the mel/sym pair as the main “lever” for monetary policy allows us to extract “inflation taxes” on sym holders in exactly the same way as paper Melmint does.

In lieu of paper Melmint’s demurrage, we introduce DOSC inflation. We keep track of an exponentially increasing DOSC inflator $\kappa$. The difficulty of creating on-chain ergs is divided by the inflator, so that each erg represents a smaller and smaller amount of real-world computation. At the same time, the targeted erg/mel exchange rate is multiplied by the inflator, so that more and more ergs are needed to obtain one mel. This has the exact same effect as demurraging a fixed DOSC, without requiring erg balances to ever change.

Specification

Melswap: a Uniswap-esque built-in DEX

The foundation of Melmint v2 is Melswap, a decentralized exchange built into Themelio that allows free exchange between any two Themelio Denoms. Melswap is an extremely simple Uniswap-like “constant product” automated market maker, and it is based on three concepts: pools, swapping, and liquidity tokens.

Pools

We keep a pool that stores liquidity for a particular token and Mel. The transaction level State has a member State::pools of type SmtMapping<PoolKey, PoolState>. A PoolKey is

pub struct PoolKey {
  pub left: Denom,
  pub right: Denom,
}

where left must be lexicographically smaller than right. This structure uses custom serialization: if either left or right is Denom::Mel, then the whole PoolKey is serialized as the other token. Otherwise, the PoolKey is serialized as 32 bytes of zeroes, plus the standard stdcode serialization for (left, right).

Note: this strange serialization is for backwards compatibility from before Melswap supported swapping between two non-Mel tokens. TIP-902 added support for non-Mel/non-Mel swapping.

Each PoolState is:

pub struct PoolState {
    pub left_tokens: u128,
    pub right_tokens: u128,
    pub price_accum: u128, // unit: lefts per right
    pub liqs: u128,
}

We call the “left” token “lefts” and the right hand token “rights” in our description.

Swapping

Swapping a involves sending a sum of either lefts or rights into a particular pool, while withdrawing the other token.

We use a transaction with kind Swap. The data field refers to a key in State::pools.

Nothing “special” happens when the transaction is applied to the state, and it is processed exactly like a transaction of type Normal.

This is because to safeguard order-independence of all transactions, the actual execution of all swaps within a block is done on block sealing — in a sense, swaps settle at the next block height rather than immediately. When a block is sealed, we settle all the swaps in the block simultaneously.

This is done by following this procedure:

• Find all transactions in this block of kind Swap, whose first output has not been spent, whose data field points to an existing pool, and whose first output’s denomination is either lefts or rights. These are the swap requests. The first output of every swap request is supposed to be swapped to its counterpart.
• For each pool mentioned in some swap request:
  • Add the first output of all swap requests for that pool, whether left or right, into the pool. Let $\Delta_\ell$ be the lefts added, $\Delta_r$ be the tokens added, $\ell$ be the original number of lefts, and $r$ be the original number of rights.
  • We compute the exchange rate of the token as simply the ratio $X=(\Delta_\ell+\ell)/(\Delta_r +r)$.
  • We add $\lfloor 10^6 X \rfloor$ to price_accum, wrapping around on overflow.
  • We compute exactly how many lefts and rights to remove from the pool: $W_\ell = \lfloor0.995X\Delta_r\rfloor,W_m=\lfloor0.995X\Delta_\alpha\rfloor$
  • We change the number of lefts in the pool to $\ell+\Delta_\ell-W_\ell$, and the number of rights to $r+\Delta_r-W_r$.
  • We settle each swap request by transmuting the CoinData binding of their first output in coins, with value $v$:
    • If the coin is is left-denominated, change denom to right, and change value to $$\left\lfloor\frac{vW_r}{\Delta_\ell}\right\rfloor$$
    • If the coin is token-denominated, change denom to µmel, and change value to $$\left\lfloor\frac{vW_\ell}{\Delta_r}\right\rfloor$$

Note: we always round down. This can lead to minute amounts of tokens “getting lost”, but we never guarantee that tokens cannot get lost anyway (they can be sent to the zero address), so it is always safe to err on the side of tokens getting lost.

Note: we use this all-at-once approach at block sealing to achieve strict order-independence. This also happily gets us a degree of frontrunning resistance.

Liquidity tokens

To reward people for depositing liquidity into a Melswap pool, we use a Uniswap-like liquidity token system. There are two kinds of transactions, LiqDeposit and LiqWithdrawal.

Similar to Swap transactions, they are processed in the “pipeline” just like Normal transactions, and their effects apply on block sealing using coin transmutation. In particular, when sealing a block, after processing swaps:

• Process deposits:

  • Find all LiqDeposit transactions in the block, whose first output’s denomination is lefts, and whose second output’s denomination is rights, neither of which have been spent.

  • For each pool, existing or nonexisting, mentioned in some LiqDeposit:

    • If the pool doesn’t exist:
      • Create a pool, with $L$ lefts and $R$ rights, where $L$ and $R$ are the total lefts and rights in the first and second outputs of the LiqDeposits for this pool.
      • For each of the LiqDeposits for this pool:
        • Given that the transaction deposits $\ell$ lefts, transmute the first output to $ \ell$ liquidity tokens. If one of the left or right tokens is Mel, then the liquidity tokens have denom $H_\mathsf{liq}(c)$, where $c$ is non-mel token’s Denom. Otherwise, the liquidity token has denom $H_\mathsf{liq}(K)$, where $K$ is the PoolKey of the pool.
        • Delete the second output from the state.
      • Set liqs of the pool to the total number of liquidity tokens created.
    • If the pool does exist:
      • Add all the mels and tokens into the pool.
      • For each of the LiqDeposits for this pool:
        • Given $\ell,r,q,\Delta_\ell,\Delta_r$, the number of liquidity tokens minted is $$\Delta_q = q\left\lfloor \sqrt{\frac{\Delta_\ell\Delta_r}{\ell r}} \right\rfloor$$
        • Update liqs and transmute accordingly.

• Process withdrawals

  • Find all LiqWithdrawal transactions in the block, whose first output’s denomination is the liquidity token of the “correct” pool, which hasn’t been spent. The data field specifies which pool it is.
  • Using exact arithmetic, compute the correct number of lefts and rights to withdraw for every liquidity token.
  • For every LiqWithdrawal transaction, transmute its first output to the floor of the correct number of lefts, and synthesize a second output to the floor of the correct number of rights.
  • Decrement liqs properly. This should never overflow because liqs can’t proliferate elsewhere.

The Melmint mechanism

Melmint is now a simple “central bank” mechanism that supplies liquidity to Melswap to loosely target a given erg/mel exchange rate. This is implemented as the following procedure on block seal, after Melswap is processed:

• Calculate the implied sym/erg exchange rate $X_{SD}$; this is just the ratio of sym to erg in the sym/erg pool.
• “Nudge” the sym/mel pool, containing $s$ syms and $m$ mels, with towards 1 mel = $\kappa$ erg worth of sym, where $\kappa$ is the DOSC inflator:
  • Compute the target ratio: $\hat{R}_{SM} = \kappa \times R_{SD}$
  • We first nudge the number of syms: $s' = \lfloor0.995s \rfloor + \lfloor 0.005(m \cdot \hat{R}_{SM}) \rfloor$
  • Now the “product” is out of whack, so we restore the product. Compute the “stretch factor” $\gamma=s'/s$ and set
    • $s \gets \lfloor s'/\lfloor\sqrt{\gamma}\rfloor \rfloor$
    • $m \gets \lfloor m\cdot \lfloor\sqrt{\gamma}\rfloor \rfloor$
  • This sets the price 1/200th closer to the “correct” exchange rate. Thus, the peg will restore “half way” in approximately 2 hours if market conditions are neutral.

Why are we so conservative with nudging the target rate? This is largely to prevent small fluctuations or market manipulation from destabilizing Melmint. As long as the market expects Melmint to eventually defend the peg, the market will likely immediately restore deviations from the peg.

We choose this approach rather than trying to use something like a 24-hour TWAP to get a manipulation-proof price feed and taking immediate action because the latter just makes manipulating the TWAP have a huge payoff, since misleading Melmint will cause immediate, catastrophic action.

Minting DOSC

DOSC minting is also done through coin transmutation. DoscMint transactions must have one output only. A second output will be synthesized in the next block with the appropriate reward.

Discussion

Why is Melmint v2 better?

Melmint v2’s design is better because:

• It is less intrusive to implement. We don’t introduce exceptions left and right to the core transaction validation logic. Instead, “coin transmutation” when the block is sealed implements all Melmint-related actions. Logic for transmuting coins can be implemented once and reused.
• It provides a general fallback DEX. This DEX is unlikely to become dominant on Themelio, especially as layer-2 solutions mature, but it nevertheless will provide a secure source of approximate market prices that always works.
• It’s much simpler conceptually, largely because it gets rid of the the two most complicated procedures in Melmint: sym auction and recovery.
• It’s most likely far more robust because it does not require complicated auction rules or hardcoded depegging mechanisms. Instead, it relies on the well-studied, battle-tested robustness of constant-product AMMs and a market-based depegging mechanism that we will discuss in the next section.

Market-based depegging

One notable feature in Melmint v2 is that the mel/sym pool is not directly funded by printing mels/syms out of thin air. Instead, the strength of Melmint’s monetary policy “lever” is decided entirely by market participants' individual decisions to contribute to the mel/sym liquidity pool.

This is important, because it actually avoids a failure scenario in Melmint v1. In v1, unless an arbitrary depegging threshold is used, a “death spiral” can form where a sudden loss of confidence in the mel causes a run on the mel as people rush to convert them into syms at an above-market price, which then hyperinflates the syms, causing even more loss of confidence in the mel, etc.

In v2, however, such a spiral cannot happen, because when there is a whiff of sym hyperinflation-induced systemic collapse, the immediate response of any rational sym holder would be to remove liquidity from the sym/mel pool to “cash out” as fast as possible. This rapidly disables Melmint’s monetary policy.

Furthermore, each marginal withdrawal marginally weakens Melmint, so there’s much less pressure to be the “first in line” to withdraw.

Thus, Melmint is inherently run-proof the way properly priced money-market mutual funds, as opposed to fractional-reserve bank accounts, are run-proof.